Riemann-von Mangoldt formula for $\zeta(s)$
asymptotics special-functions complex-analysisIn 1859, famous mathematician Georg Friedrich Bernhard Riemann conjectured Riemann hypothesis that
All nontrivial zeros of $\zeta(s)$ lie on the line $\Re s=\frac12$
Although this hypothesis is not yet proven today, we can still investigate other parts of Riemann's paper. In particular, we want to derive the following asymptotic formula:
\[N(T)={T\over2\pi}\log{T\over2\pi}-{T\over2\pi}+\mathcal O(\log T)\]where $N(T)$ is the zero-counting function for $\zeta(s)$:
\[N(T)\triangleq\sum_{0<\Im\rho\le T}1\]Before diving into $\zeta(s)$, let's first see how we can actually count the zeros.
Argument principle
One way to count is by applying Jensen's formula. However, Jensen's formula only gives a rough inequality and is more suitable to count zeros in circular regions. As a result, a more precise and flexible tool is needed.
Jensen's formula mainly extracts information about zeros using logarithms, so we can intuitively try to take out similar information using the logarithmic derivative. If $z_1,z_2,z_3,\dots,z_m$ (counted with multiplicities) are the zeros of some analytic function $f(z)$ within region $D$, then by taking logarithmic derivative we know that the following function
\[g(z)={f'\over f}(z)-\sum_{k=1}^m{1\over z-z_k}\]is analytic within $D$. In addition, if $\partial D$ is oriented in a counterclockwise direction and $f(z)$ is nonzero on $\partial D$, we can apply residue theorem to get
\[{1\over2\pi i}\oint_{\partial D}{f'\over f}(z)\mathrm dz={1\over2\pi i}\oint_{\partial D}g(z)\mathrm dz+\sum_{k=1}^m\oint_{\partial D}{\mathrm dz\over z-z_k}\]Because $g(z)$ is analytic in $D$ and on $\partial D$, the first integral on the right is guaranteed to be zero. Moreover, by residue theorem we also know that the summation equals to $m$. Therefore, we successfully obtain an exact formula for us to count zeros (also known as argument principle):
\[{1\over2\pi i}\int_{\partial D}{f'\over f}(z)\mathrm dz=\#\{\text{Zeros of $f(z)$ in $D$ counted with multiplicities}\}\]Selecting contour
According to a previous article, we know that Riemann xi function defined by
\[\xi(s)=\frac12s(s-1)\pi^{-s/2}\Gamma\left(\frac s2\right)\zeta(s)\tag1\]is an entire function that does not have trivial zeros, so counting the zeros of $\xi(s)$ is equivalent to counting the nontrivial zeros of $\zeta(s)$. Now, let's build up a contour to enclose the critical strip for us to count zeros:
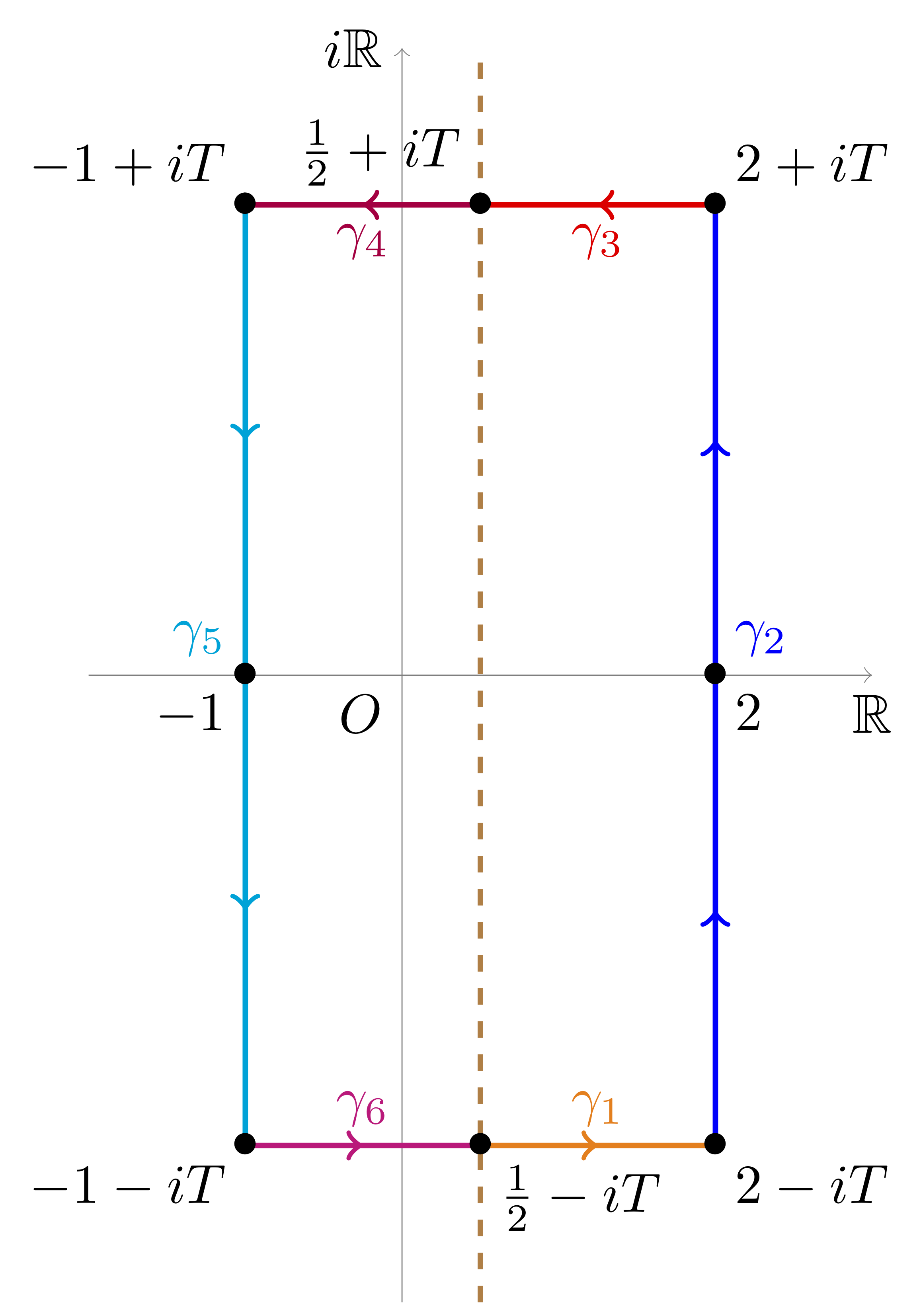
Due to the functional equation $\xi(s)=\xi(1-s)$. a zero $\rho$ on the upper half region is accompanied by another zero $1-\rho$ on the lower half region. Consequently, the number of zeros enclosed by the above contour $\gamma$ is twice the number of zeros on the upper half portion. Mathematically speaking, we have
\[2N(T)={1\over2\pi i}\oint_\gamma{\xi'\over\xi}(s)\mathrm ds\]Furthermore, the functional equation implies the symmetric relationship about the critical line:
\[{\xi'\over\xi}(s)=-{\xi'\over\xi}(1-s)\]By applying this relationship to each of the contours, we can discover
\[\int_{\gamma_1+\gamma_2+\gamma_3}{\xi'\over\xi}(s)\mathrm ds=\int_{\gamma_4+\gamma_5+\gamma_6}{\xi'\over\xi}(s)\mathrm ds\]This means that if we were to define $C=\gamma_1+\gamma_2+\gamma_3$ then
\[N(T)={1\over2\pi i}\int_C{\xi'\over\xi}(s)\mathrm ds\tag2\]Basic expansion
To proceed, let's plug in (1) to get
\[{\xi'\over\xi}(s)={\mathrm d\over\mathrm ds}\log{s(s-1)\over2}+{\mathrm d\over\mathrm ds}\log\left[\Gamma\left(\frac s2\right)\pi^{-s/2}\right]+{\zeta'\over\zeta}(s)\]Plugging this into (2), we have
\[\begin{aligned} {1\over2\pi i}\int_C{\mathrm d\over\mathrm ds}\log{s(s-1)\over2}\mathrm ds &={1\over2\pi i}\left.\log{s(s-1)\over2}\right \vert _{1/2-iT}^{1/2+iT} \\ &=\frac1\pi\Im\log{(1/2+iT)(-1/2+iT)\over2} \\ &=\frac1\pi\arg{-T^2-1/4\over2}=1 \end{aligned}\] \[\begin{aligned} {1\over2\pi i}\int_C{\mathrm d\over\mathrm ds}\log\left[\Gamma\left(\frac s2\right)\pi^{-s/2}\right]\mathrm ds &=\left.{1\over2\pi i}\log\left[\Gamma\left(\frac s2\right)\pi^{-s/2}\right]\right \vert _{1/2-iT}^{1/2+iT} \\ &=\left.\frac1\pi\Im\log\left[\Gamma\left(\frac s2\right)\pi^{-s/2}\right]\right \vert _{1/2+iT} \\ &=\frac1\pi\arg\left[\Gamma\left(\frac14+{iT\over2}\right)\right]-\frac T2\log\pi \end{aligned}\]Consequently, putting these altogether gives
\[N(T)=\frac1\pi\arg\left[\Gamma\left(\frac14+{iT\over2}\right)\right]-\frac T2\log\pi+S(T)\]in which $S(T)={1\over2\pi i}\int_C{\zeta'\over\zeta}(s)\mathrm ds$.
Handling the Gamma term
The argument of the Gamma function does not explicit tell the growth of $N(T)$, and because argument is often associated with logarithms, we can apply Stirling's formula here:
\[\begin{aligned} \log\Gamma\left(\frac14+{iT\over2}\right) &=\left({iT\over2}-\frac14\right)\log\left(\frac14+{iT\over2}\right)-\frac14-{iT\over2}+\frac12\log2\pi-\int_0^\infty{\overline B_1(x)\over 1/4+iT/2+x}\mathrm dx \end{aligned}\]Taking the imaginary parts, we have
\[\begin{aligned} \arg\Gamma\left(\frac14+{iT\over2}\right) &=\frac T2\log\left \vert \frac14+{iT\over2}\right \vert -\frac14\arg\left(\frac14+{iT\over2}\right) \\ &-\frac T2-\Im\int_0^\infty{\overline B_1(x)(1/4+x-iT/2)\over(1/4+x)^2+(T/2)^2}\mathrm dx \\ &=\frac T2\log\frac T2+\frac T2\left \vert 1/4+iT/2\over T/2\right \vert -\frac14\arctan(2T) \\ &-\frac T2+\frac T2\int_0^\infty{\overline B_1(x)\over(T/2)^2+(x+1/4)^2}\mathrm dx \\ &=\frac T2\log\frac T2-\frac T2+\frac T4\log\left(1+{1\over4T^2}\right) \\ &+\frac14\left[\arctan\left(1\over2T\right)-\frac\pi2\right]+\frac T2\int_0^\infty{\overline B_1(x)\over(T/2)^2+(x+1/4)^2}\mathrm dx \\ &=\frac T2\log\frac T2-\frac T2-\frac\pi8+\delta(T) \end{aligned}\]in which the remainder term $\delta(T)$ is defined by
\[\delta(T)=\frac T4\log\left(1+{1\over4T^2}\right)+\frac14\arctan\left(1\over2T\right)+\frac T2\int_0^\infty{\overline B_1(x)\over(T/2)^2+(x+1/4)^2}\mathrm dx\]Riemann-von Mangoldt formula
With everything ready, we combine our results and eventually arrived at the Riemann-von Mangoldt formula for $\zeta(s)$.
\[N(T)={T\over2\pi}\log{T\over2\pi}-{T\over2\pi}+\frac78+S(T)+\frac1\pi\delta(T)\]By the characteristics of logarithms and inverse tangents, we can easily see that $\delta(T)$ is of $\mathcal O(1/T)$.
Summary
In this article, we begin with developing a technique to analyze the zero distribution of analytic functions in arbitrary regions. Then, we apply this technique to $\xi(s)$ and obtain a simple formula to understand the growth of $N(T)$. However, this is not yet finished since more information must be extracted from $S(T)$ before concluding with an asymptotic estimate, and these will be covered in subsequent blogs. I have also opened a question regarding $S(T)$ on Math Stackexchange, feel free to discuss!
References
- Dittrich, W. (2018). Reassessing Riemann’s Paper.
- Edwards, H. M. (1974). Riemann’s Zeta Function.
- Karatsuba, A. A. (1990). The distribution of prime numbers. Russian Mathematical Surveys, 45(5), 99–171.
- Tenenbaum, G. (1995). Introduction to Analytic and Probabilistic Number Theory.