Alternative Approach to Redefine $\zeta(s)$
special-functions complex-analysisAn integral formula for the critical strip
In the previous article, we have derived
\[\zeta(s)=\sum_{k=1}^M{1\over k^s}+{M^{1-s}\over s-1}-{1\over2M^s}-s\int_M^\infty{P_1(t)\over t^{s+1}}\mathrm dt\]in which $P_1(t)={t}-1/2$ is the first Bernoulli function. If we set $M=1$, we get
\[\zeta(s)=\frac12+{1\over s-1}-s\int_1^\infty{P_1(t)\over t^{s+1}}\mathrm dt\tag1\]By integration by parts, we can see that
\[\int_1^\infty{P_1(t)\over t^{s+1}}\mathrm d t=\left.{P_2(t)\over2t^{s+1}}\right|_1^\infty+{s+1\over2}\int{P_2(t)\over t^{s+2}}\mathrm dt\]Because periodic Bernoulli polynomials are bounded, the integral on the right hand side converges for all $\Re s>-1$, meaning that the integral on the right of (1) converges for all $\Re s>-1$. This demonstrates that (1) expands the domain of $\zeta(s)$ from $\Re s>1$ to $\Re s>-1$. Moreover, if $-1<\Re s<0$, we can use the fact that
\[-s\int_0^1{P_1(t)\over t^{s+1}}\mathrm dt=\frac12+{1\over s-1}\]to obtain an integral formula for $\zeta(s)$ within $-1<\Re s<0$:
\[\zeta(s)=-s\int_0^\infty{P_1(t)\over t^{s+1}}\mathrm dt\tag2\]This also indicates that our task becomes to analytically continue the integral on the RHS.
Fourier expansion of $P_1(t)$
Because fractional part function ${t}$ is not a convenient tool for us to work, we want to find an alternative expression to break it down. Thus, by its periodicity, we try to Fourier expand ${t}$ on the interval $[0,1]$:
\[\{t\}=\sum_{n\in\mathbb Z}c_ne^{2\pi int}\tag3\]Now, using the classical theory of Fourier series, we have
\[c_n=\int_0^1\{t\}e^{-2\pi int}\mathrm dt\]Consequently, we obtain that at $n=0$
\[c_0=\int_0^1\{t\}\mathrm dt=\left.{t^2\over2}\right|_0^1=\frac12\]and for $n\ne0$:
\[\begin{aligned} c_n &=\int_0^1te^{-2\pi int}\mathrm dt \\ &=\left[{te^{-2\pi int}\over-2\pi in}\right]_0^1+{1\over2\pi in}\int_0^1e^{-2\pi int}\mathrm dt \\ &=-{1\over2\pi in} \end{aligned}\]Pluggin these results into (3), we deduce
\[\begin{aligned} \{t\} &=c_0+\sum_{m=1}^\infty(c_m+c_{-m}) \\ &=\frac12-\sum_{m=1}^\infty{e^{2\pi imt}-e^{-2\pi imt}\over2\pi im} \\ &=\frac12-\sum_{m=1}^\infty{\sin(2\pi mt)\over\pi m} \end{aligned}\]which, combined with $P_1(t)$'s definition, becomes
\[P_1(t)=-\sum_{m=1}^\infty{\sin(2\pi mt)\over\pi m}\tag4\]Expanding $\zeta(s)$ into trigonometric series
Plugging (4) into (2), we have
\[\zeta(s)=s\int_0^\infty\sum_{m=1}^\infty{\sin(2\pi mt)\over\pi m}\cdot{\mathrm dt\over t^{s+1}}\]Now, set $x=2\pi mt$, so that
\[\begin{aligned} \zeta(s) &=s\int_0^\infty\sum_{m=1}^\infty{(2\pi m)^s\over\pi m}{\sin x\over x^{s+1}}\mathrm dx \\ &=2^s\pi^{s-1}\int_0^\infty\sum_{m=1}^\infty{1\over m^{1-s}}{\sin x\over x^{s+1}}\mathrm dx \\ &=2^s\pi^{s-1}\zeta(1-s)\int_0^\infty{\sin x\over x^{s+1}}\mathrm dx \end{aligned}\]As a result, to continue we must take down the remaining integral:
\[\int_0^\infty{\sin x\over x^{s+1}}\mathrm dx\tag5\]Laplace transform of power functions
Because sine can always be decomposed into complex exponentials
\[\sin\theta={e^{i\theta}-e^{-i\theta}\over2i}\]we can take down (5) by evaluating
\[\int_0^\infty{e^{\pm ix}\over x^{s+1}}\mathrm dx\]This actually reminds me of a commonly used Laplace transform identity:
\[{\Gamma(a)\over\lambda^a}=\int_0^\infty t^{a-1}e^{-\lambda t}\mathrm dt\tag6\]Originally this expression only works for positive real $\lambda$, but if we apply (6) as though it works for $\arg\lambda\in[-\pi/2,\pi/2]$ we have
\[\int_0^\infty{e^{\pm ix}\over x^{s+1}}\mathrm dx=(\mp i)^s\Gamma(-s)=e^{\mp\pi is/2}\Gamma(-s)\tag7\]Justification of (7) using complex analysis
Consider the following integral
\[\int_{\gamma(\theta)}{e^{-z}\over z^{s+1}}\mathrm dz\tag8\]where the path $\gamma(\theta)$ is a ray that starts from origin with angle $\theta$. Mathematically, we can express it as follows
\[\gamma(\theta):z=te^{i\theta},t:0\to\infty\]and we will prove the integral does not depend on $\theta$ whenever $-\pi/2\le\theta\le\pi/2$.
Without loss of generality, let $-\pi/2\le\alpha<\beta\le\pi/2$ and build up a pie-like contour as follows:
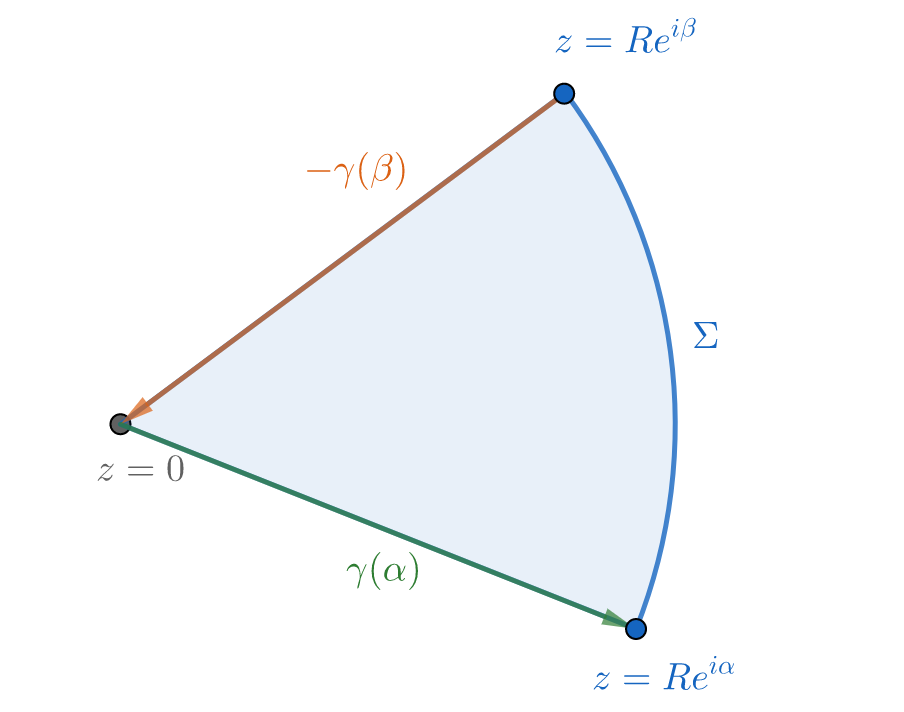
Since the integrand is analytic within the blue region, it follows from Cauchy's integral theorem that
\[\int_{\color{orange}{\gamma(\beta)}}=\int_{\color{green}{\gamma(\alpha)}}+\int_\Sigma\]However, as $R$ goes to infinity we have
\[\begin{aligned} \left\vert\int_\Sigma\right\vert &\le\int_\alpha^\beta{e^{-R\cos\phi}\over R^{\Re s}}\mathrm d\phi \\ &={(\beta-\alpha)e^{-R\cos\varphi}\over R^{\Re s}}\quad{\varphi\in(\alpha,\beta)} \\ \end{aligned}\]Because $\cos\varphi<0$, we see that this integral will vanish. Thus for all $-\pi/2\le\theta\le\pi/2$
\[\int_{\gamma(\theta)}=\int_{\gamma(0)}=\Gamma(-s)\]This appears to be unrelated to the original integral we are dealing with, but we can set $\theta=\pm\pi/2$ to get
\[\int_{\gamma(\pm\pi/2)}=\int_0^\infty(e^{\pm i\pi/2}t)^{-s-1}e^{\mp it}\mathrm dt=-\Gamma(-s)\]Simplification will result in (7).
Proof of the functional equation
Equation (7) indicates that (5) satisfies
\[\begin{aligned} \int_0^\infty{\sin x\over x^{s+1}}\mathrm dx &={1\over2i}\int_0^\infty{e^{ix}-e^{-ix}\over x^{s+1}}\mathrm dx \\ &=\Gamma(-s){e^{-\pi is/2}-e^{\pi is/2}\over2i} \\ &=-\sin\left(\pi s\over2\right)\Gamma(-s) \end{aligned}\]As a result, $\zeta(s)$ becomes
\[\zeta(s)=2^s\pi^{-s}\zeta(1-s)(-s)\sin\left(\pi s\over2\right)\Gamma(-s)\]Now, by the functional equation that $\Gamma(z+1)=z\Gamma(z)$, we finally obtain the functional equation for Riemann zeta function:
\[\zeta(s)=2^s\pi^{s-1}\sin\left(\pi s\over2\right)\Gamma(1-s)\zeta(1-s)\]Summary
In this article, we perform analytic continuation on Riemann zeta function by Fourier expansion on the fractional part function.
Although I accidentally discovered this, it was already discovered 70 years ago after I read more books :-(. Particularly, I found a similar method in chapter 2 of Titchmarsh and Health-Brown's The theory of Riemann-zeta function. Ah-huh, I always rediscover previous works on the way :D